Regression by Sampling

Code can be found at: https://github.com/statswithrdotcom/Regression-by-Sampling

In the world of big data, we may encounter situations where we can not store the data set and calculations required for regression models in random access memory (RAM). Although this is rare, as modern computer RAM capacities can generally handle large datasets, it can sometimes be necessary to estimate regression parameters by sampling from the data set of interest. In this tutorial, I am going to show you how to do just that. We are going to be estimating the coefficients for a data set containing 10^8 rows, by sampling 100 rows, and calculating the coefficients for multiple samples. So let’s get started by generating the data. Note that, by design, the true population values are 4 for the intercept, 3 for coefficient 1, 2 for coefficient 2, and 1 for coefficient 3. This means that the true population values in our output are 4, 3, 2, 1.

# Size of the data set
N = 10^8

# Number of rows sampled
Sample_Size = 100

# Number of times a sample is taken
Runs = 100

# Creating dummy variables
X1 = rnorm(N)
X2 = rnorm(N)
X3 = rnorm(N)

# Defining a dummy outcome variable
Y = 3*X1 + 2*X2 + X3 + 4 + rnorm(N)

Now, I am going to create an empty matrix that will store the regression coefficients for each sample of 100 rows taken. The “Runs” variable tells the loop how many times the data set should be sampled from and estimates generated. The ncol is set equal to 4, because we will be given 4 coefficients including the intercept.

# Setting up an empty matrix
Estimates <- matrix(0, nrow = Runs, ncol = 4)

# Fills the estimates matrix with coefficients calculated from the samples
for(i in 1:Runs){
Ind = sample(1:N, size = Sample_Size, replace = TRUE)
Estimates[i,] <- summary(lm(Y[Ind] ~ X1[Ind] + X2[Ind] + X3[Ind]))$coefficients[,1]
}

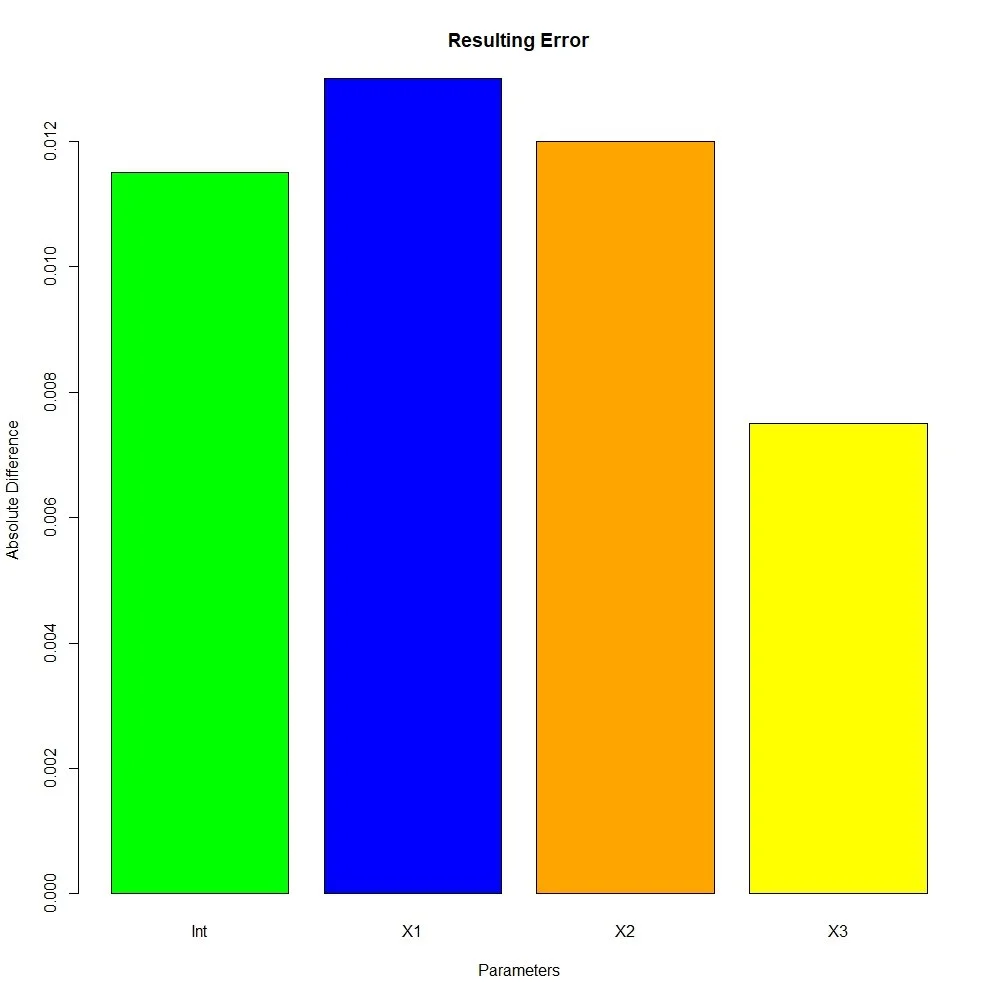
We now have a matrix of estimates, with each row corresponding to the coefficients generated from doing a regression on 100 randomly sampled rows from the larger data set. Before we go further I am going to make a small helper function that calculates absolute value difference, which I am going to loosely call error. Now, with the help of the apply function, we can get the average coefficient estimates, that are close to the true population value. As you can see, I also wrote a line of code that will print the absolute value error associated with each coefficient. You can also refer to the bar plot below, although the coefficients will change because I did not use set.seed().

# A simple function that takes the absolute value difference of two inputs
Error <- function(x,y){return(round(abs(x-y),4))}

# Calculates the real estimates and prints the difference from the true values
Est <- apply(Estimates, MARGIN = 2, FUN = mean)
print(paste("Int Error =", Error(Est[1],4)," X1 Error =", Error(Est[2],3),
" X2 Error =",Error(Est[3],2)," X3 Error =",Error(Est[4],1)))

If you have read anything else I have written, you probably know that I love wrapping code into functions. So that is what I am going to do! This function allows you to automate the process, with the addition of confidence intervals (CIs) for the population value. Much of the extra code was to ensure that the output is formatted correctly regardless of which options you choose. Additionally, I put some effort into verifying that the confidence intervals are correct when Runs = 100 and Sample Size = 100. By correct, I mean that 95% confidence intervals capture the true population value 95% of the time. To my knowledge, the CIs are correct with those settings, although you may want to verify that for yourself if Runs and Sample Size are changed. If you are not verifying that your CIs are correct, you can simply use the “One if Correct” row to mean “One if 0 is included in the interval” as the “correct” values are defaulted to 0.

Reg_Sampler <- function(Equation, Data, Runs = 100, Sample_Size = 100, Confidence = 1.96, Decimals = 3, Correct_Values = -99){

# Samples the data and creates a data frame of estimated coefficients
Estimates <- matrix(0, nrow = Runs, ncol = length(summary(lm(Equation, data = Data[1:ncol(Data),]))$coefficients[,1]))
for(i in 1:Runs){
Ind = sample(1:nrow(Data), size = Sample_Size, replace = TRUE)
Estimates[i,] <- summary(lm(Equation, data = Data[Ind,]))$coefficients[,1]
}

# Takes the mean and standard deviation of coefficient estimates
Est <- apply(Estimates, MARGIN = 2, FUN = mean)
sd <- apply(Estimates, MARGIN = 2, FUN = sd)

# Constructs confidence Intervals (that are validated as correct later)
Intervals <- rep(0,length(Est))
for(i in 1:length(Est)){
Intervals[i] <- paste(round(Est[i]-Confidence*sd[i]*(1/sqrt(Runs)),Decimals),
"to",round(Est[i]+Confidence*sd[i]*(1/sqrt(Runs)),Decimals))
}

# This allows someone to specify the parameter values if known (for validation)
if(Correct_Values[1] == -99){
Correct_Values = rep(0,length(Est))
print("No correct values supplied, which defaulted to 0!")
}

# This notes in the output if the confidence interval correctly captured the parameter
Correct_Int = rep(0,length(Est))
for(i in 1:length(Est)){
if(round(Est[i]-Confidence*sd[i]*(1/sqrt(Runs)),Decimals) <= Correct_Values[i] &
round(Est[i]+Confidence*sd[i]*(1/sqrt(Runs)),Decimals) >= Correct_Values[i]){
Correct_Int[i] = 1
}
}

# The code below simply organizes and formats the output of the function
Output <- data.frame(rbind(Est,Intervals,as.numeric(Correct_Int)))
if(ncol(Output) > 1){names(Output) <- c("Intercept",paste("Coef",1:(ncol(Output)-1)))}
if(ncol(Output) == 1){names(Output) <- "Intercept"}
row.names(Output) <- c("Point Estimate", "Confidence Interval", "One if Correct")
return(Output)
}

# Note that the intercept can be removed, but the column names will be made incorrect!
Reg_Sampler(Equation = Y ~ X1 + X2 + X3, Data = data.frame(X1,X2,X3,Y), Runs = 100, Sample_Size = 100)

If interested, here is the code I used for the validation that my 95% CIs actually do capture the true parameter 95% of the time. Note that this is computationally intensive, as you are forced to do N*Runs regressions.

# This function validates that the percentage of correct confidence intervals are what we expect.
# The default number of replications, N, is 100 because it can take a while to compute.
# With an N of 10,000 I obtained values of 0.9555, 0.9511, 0.9499, and 0.9488 showing that they are in fact 95% CIs.

Validation_Fun <- function(N = 100, Correct = 4:1, Conf = 1.96){
Test_Frame = matrix(0, nrow=N, ncol=4)
for(i in 1:N){
Test_Frame[i,] = as.matrix(as.numeric(Reg_Sampler(Equation = Y ~ X1 + X2 + X3, Confidence = Conf, Data = data.frame(X1,X2,X3,Y), Runs = 100, Sample_Size = 100, Correct_Values = Correct)[3,]))
}
return(apply(Test_Frame, MARGIN = 2, FUN = mean))
}

Validation_Fun()